We discovered in Geometry class that if you happen to sum the sq. of two sides of a triangle and take its sq. root, you’ll have the aspect of the hypotenuse or the third aspect. This, known as as Pythagorean theorem form of holds a everlasting place in our minds. Nevertheless, distances might be way more difficult and might take many various types equivalent to geometrical, computational, statistical distances and so forth. On this article, we’re going to have a look at a number of the most vital distance metrics used within the subject of Machine Studying. So, let’s get began.
#1. Euclidean Distance
Because the crow flies.
— Outdated Saying
Euclidean distance is probably probably the most intuitive distance metric. It measures the straight-line distance between two factors in a multidimensional area.
Should you think about two factors on a airplane, the Euclidean distance is the size of the road section connecting them. That is calculated utilizing the Pythagorean theorem.
This simple metric works properly in circumstances the place the size have the identical unit of measure and are scaled equally.
Nevertheless, Euclidean distance has its limitations. As an example, when information has outliers or when the significance of various dimensions varies, Euclidean distance may not be the only option. Additionally, it doesn’t carry out properly in high-dimensional areas, a phenomenon referred to as the “curse of dimensionality.”
#2. Manhattan Distance
Manhattan distance, often known as “Taxicab” or “L1 distance,” measures the space between two factors by solely shifting alongside the axes, as if driving by a grid of streets. In contrast to Euclidean distance, which calculates the shortest path, Manhattan distance calculates the trail primarily based on a sequence of right-angle turns.
Think about navigating a metropolis the place you may solely transfer alongside the streets, making proper turns. That is depicted within the picture, the place the trail(blue) zigzags alongside the grid.
Manhattan distance can be utilized in circumstances of discrete optimisation issues the place you might be constrained by edges or in traversal of a graph.
Should you contemplate the issue of housing value evaluation, you’d almost definitely need to measure the worth of homes which might be shut by driving and never by flying. In any other case you may embrace homes which might be throughout a barrier like a lake or mountain. That might be humorous.
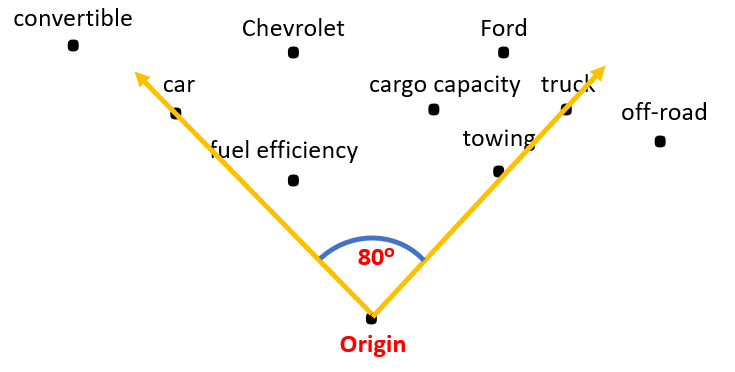
#3. Cosine Similarity
Cosine similarity measures the cosine of the angle between two vectors in a multidimensional area. It’s particularly helpful in textual content evaluation and data retrieval.
The picture reveals the angle between two vectors representing a automotive and a truck, with factors surrounding them indicating the related options. The smaller the angle, the upper the similarity between the 2 vectors. A famous example is the “king-queen” analogy in word embeddings, the place “king” and “queen” have a excessive cosine similarity regardless of completely different magnitudes (e.g., “man” + “girl” = “queen”).
In cosine similarity we’re solely within the angle between the vectors and never the magnitude, making it a most well-liked selection in high-dimensional textual content information the place the frequency of phrases might fluctuate enormously.
#4. Minkowski Distance
Minkowski distance is a generalization of each Euclidean and Manhattan distances. It introduces a parameter p that determines the kind of distance:
The place:
- p=1 provides the Manhattan distance.
- p=2 provides the Euclidean distance.
- p > 2 provides extra common distances relying on p.
The diagram illustrates how various p modifications the form of the “unit ball” (set of all factors inside a distance of 1 from a central level, outlined by a particular distance metric) round a degree. Decrease values of p create sharper, star-like shapes, whereas greater values create rounder, smoother shapes.
This flexibility means that you can modify the sensitivity to completely different dimensions in your dataset, making it helpful in numerous use circumstances like Clustering, Classification, and so on.
#5. Jaccard Distance
Jaccard distance is a measure of dissimilarity between two units. It’s outlined as one minus the Jaccard index, which is the dimensions of the intersection divided by the dimensions of the union of the pattern units.
That is primarily used to shortly decide how dissimilar two strings/paperwork are primarily based on their character/phrase units. A better worth means the strings/paperwork are extra completely different and vice versa.
Jaccard distance is good for functions like textual content mining in paperwork, or in circumstances the place you’re evaluating binary information (e.g., presence or absence of a characteristic).