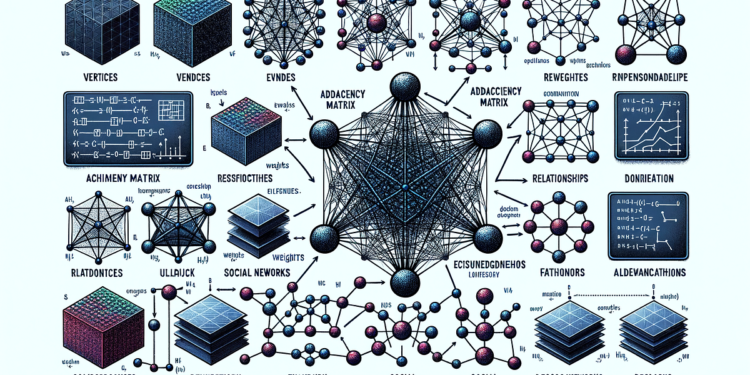
Graph theory is a pivotal branch of mathematics focusing on the study of graphs, which are structures that model relationships and connections between objects. These objects, known as vertices or nodes, are interconnected by edges, which depict various forms of relationships. Understanding graph theory is essential not only for mathematical studies but also for addressing complex problems in various fields, including computer science, transportation, social networks, biology, and more. By providing a framework for representing complex datasets visually, graph theory allows researchers and practitioners to analyze relationships, derive insights, and make informed decisions based on connectivity. In this article, we will delve into core aspects of graph theory, including properties, concepts, and algorithms, emphasizing their significance and applications in real-world scenarios.
Equipped with this foundational knowledge, readers will be better prepared to explore advanced topics like graph neural networks and other cutting-edge applications. Understanding graph properties such as how nodes are connected, the weights of edges, and the overall structure of a graph can significantly influence the effectiveness of analytical techniques. Moreover, we will cover the types of graphs that exist, key properties such as connectivity and weights…